深入研究 LIME 的本地解释

本地可解释模型--不可知论解释（LIME）的直觉、理论和代码

LIME 是XAI方法的起源。它让我们了解机器学习模型的工作原理。具体来说，它可以帮助我们了解个体预测是如何做出的（即局部解释）。

尽管最近的进展意味着 LIME 不那么受欢迎，但它仍然值得了解。这是因为它是一种相对简单的方法，对于许多可解释性问题来说“足够好”。它也是一种较新的局部可解释性方法——SHAP 的灵感来源。

因此我们将：

• 讨论 LIME 为获取本地解释而采取的步骤。
• 详细讨论与这些步骤相关的一些选择，包括如何加权样本以及使用哪个替代模型。
• 应用lime Python 包：https://github.com/marcotcr/lime。

在此过程中，我们将该方法与 SHAP 进行比较。这是为了更好地了解它的缺点。我们还将看到，尽管 LIME 是一种局部方法，但我们仍然可以聚合 lime 权重以获得全局解释。这样做将有助于我们了解该软件包做出的一些默认选择。

LIME 算法

机器学习模型是复杂的函数。LIME 背后的理念是，如果我们放大实例周围区域的特征空间，这种复杂性就会消失。该函数要简单得多，甚至是线性的。这使我们能够通过对实例的排列构建简单模型来了解如何在此区域进行预测。

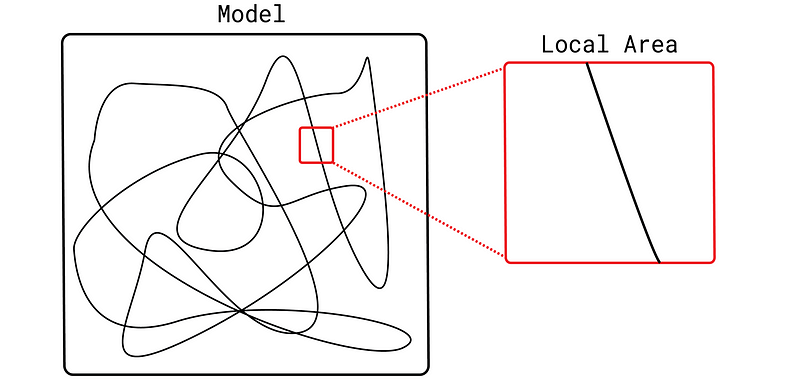
这些简单模型被称为替代模型。这些模型必须是本质上可解释的模型，如决策树或线性回归。这一点很重要，因为我们可以通过直接查看这些模型的结构或参数来了解它们的工作原理。

现在，我们有很多选择来构建这样的替代模型。下面我们讨论最重要的一些。首先，让我们总结一下 LIME 算法所采取的步骤：

1. 选择你要解释的实例
2. 通过排列特征值来生成样本
3. 根据样本与实例的距离为每个样本分配一个权重
4. 使用原始黑盒模型对这些排列进行预测
5. 使用加权样本和预测作为目标变量来训练替代模型
6. 解释替代模型

结果是一个针对单个实例进行训练的简单替代模型。通过解释这个模型，我们可以了解原始黑盒模型如何对该实例进行预测。一个关键的好处是，这是以与模型无关的方式完成的。由于我们只考虑黑盒模型预测，我们可以将此方法应用于任何机器学习算法。

排列特征值

排列对于许多 XAI 方法来说都很重要。然而，LIME 对排列特征重要性、PDP 或 ALE 采用了不同的方法。即：

• 对于连续特征，我们从具有与特征相同的均值和标准差的正态分布中抽样。
• 对于分类特征，我们根据训练数据中观察到的比例随机选择类别。

重要的是，这将为我们提供与黑盒模型训练时相似的特征值。它还让我们能够灵活地决定可以创建多少个样本。默认情况下，LIME 包中将其设置为 5000。这通常足以训练线性回归等模型。

加权样本

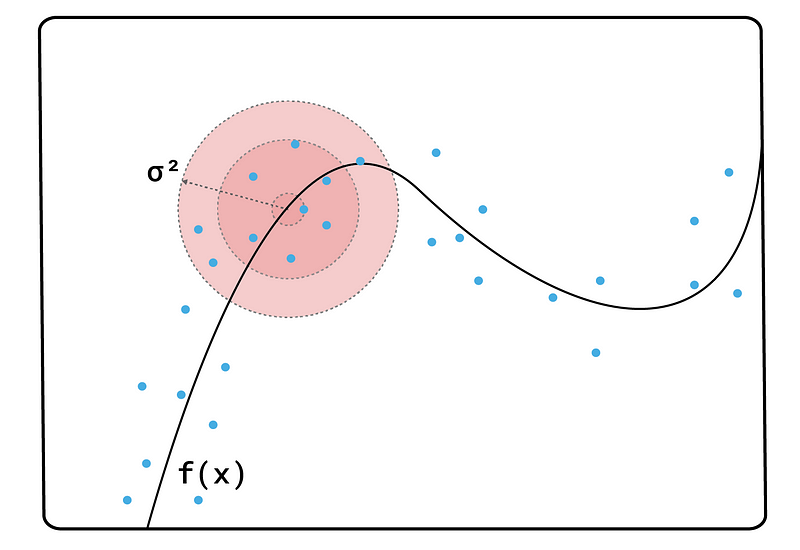
上述过程将在整个特征空间中生成样本。然而，我们感兴趣的是模型在实例周围的表现。这就是为什么我们需要根据样本与实例的距离对样本进行加权。为此，LIME 使用高斯核： \[ K(x, x') = exp(-\frac{||x-x'||^2}{\sigma^2}) \] 这里 \(x\) 是被解释的实例，\(x'\) 是我们要加权的样本。\(||x — x'||\) 是归一化特征值的欧几里得距离。对于分类特征，使用特征的单次编码来计算距离。\(σ²\) 称为核宽度。它控制分配给扰动样本的权重随着与被解释实例的距离增加而减少的速度。

默认情况下，核宽度设置为 \(0.75 * sqrt\)（特征数量）。我们可以更改此值，但不清楚对于给定问题，哪个值最适合。如图 1 所示，如果我们将 \(σ²\) 设置得太小，那么只有非常接近实例的样本才会获得显著的权重。因此，我们将无法捕捉到特征值中的足够变化，以了解它们如何影响预测。太大，关系就不再是线性的。

特征数量

我们不需要在黑盒模型使用的所有特征上训练我们的代理模型。特别是线性代理模型只能处理有限的数量。我们可以决定解释中使用的特征数量，其默认值最多为 10。如果我们选择的数字小于原始特征的数量，我们还需要选择一种选择算法（例如前向选择）。

离散化

连续特征的另一种选择是，是否根据分位数或十分位数将它们分组。这称为离散化。我们将在应用 lime 包时看到，默认情况下，所有数值特征都将按其分位数分组。这是为了更容易为这些特征提供解释。

替代模型

最后，我们可以选择使用什么模型作为替代模型。默认模型是岭回归，但我们可以使用其他类型的线性回归，甚至是决策树。请记住，模型必须是可解释的。对于线性模型，每个特征的系数告诉我们该特征对我们想要解释的预测有何贡献。

最初，所有这些选择似乎都是一件好事。然而，这导致了 LIME 最大的弱点——解释不一致。这种灵活性让我们陷入了一种 P-hacking 形式，因为我们可以操纵变量，直到得到我们想要的解释。对于那些没有良好领域知识的人来说，判断一个解释是否合理可能也很困难。

LIME 也“不一致”。这意味着如果我们调整模型，使与特征的关系发生变化，LIME 权重不一定会以反映这种变化的方式发生变化。例如，假设我们将模型从 M1 更改为 M2。现在，特征可能会比以前更多地增加预测。但是，我们不一定能够使用 LIME 来判断这一点。

克服这些弱点是 SHAP 如此受欢迎的原因之一。该方法基于Shapley 值背后的理论。这为局部可解释性方法带来了一些理想的特性。SHAP 值本质上是一致的。由于 Shapley 值的计算方式缺乏灵活性，因此操纵结果也更加困难。

lime 包的应用

现在，让我们将这一理论应用于实际。我们将应用 LIME 包，然后汇总 LIME 权重以提供全局解释。我们将看到，我们必须创建自己的函数来创建像平均 LIME 权重或蜂群这样的图。这是 SHAP 受欢迎的另一个关键原因——该包为你提供了这些图。

我们从导入开始。由于我们处理的是表格数据，因此我们使用 LimeTabularExplainer 函数（第 7 行）。

# 导入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

从sklearn.ensemble导入RandomForestRegressor
从lime.lime_tabular导入LimeTabularExplainer

数据和模型

我们将使用abalone 数据集：https://archive.ics.uci.edu/dataset/1/abalone(CC BY 4.0)。abalone(鲍鱼) 是一种美味的贝类。我们想利用壳重和去壳重量（肉的重量）等特征来预测其壳中的环数。

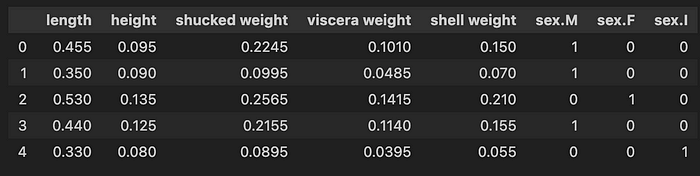
我们加载数据集（第 2-4 行）并选择目标（第 6 行）。我们还进行了一些特征工程。首先，我们排除一些高度相关的特征（第 7 行）。这是因为它们与其他特征的相关性为 1。最后，我们为性别特征创建单次编码（第 10-13 行）。你可以在 图 2 中看到最终特征集的快照。我们总共有 8 个特征。

#导入数据集
data = pd.read_csv(path_data + "/鲍鱼.data",
                  names=["sex","length","diameter","height","whole weight",
                         "shucked weight","viscera weight","shell weight","rings"])

y = data["rings"]
X = data[["sex", "length", "height", "shucked weight", "viscera weight", "shell weight"]]

# Create dummy variables
X['sex.M'] = [1 if s == 'M' else 0 for s in X['sex']]
X['sex.F'] = [1 if s == 'F' else 0 for s in X['sex']]
X['sex.I'] = [1 if s == 'I' else 0 for s in X['sex']]
X = X.drop('sex', axis=1)

X.head()

我们使用这些特征来训练模型来预测环的数量（第 2-3 行）。在本例中，我们使用了随机森林。但是，请记住 LIME 与模型无关。这意味着你应该能够将其与大多数建模包一起使用。

# 训练模型
model = RandomForestRegressor()
model.fit(X, y)

本地解释

要创建本地解释，我们首先要创建一个 LIME 解释器（第 2-6 行）。我们传入 X 特征矩阵、特征名称和目标变量名称。我们让包知道我们有一个回归模型（第 5 行），并设置随机状态（第 6 行），以便每次新运行都能获得相同的结果。

# 创建解释器
explainer = LimeTabularExplainer(X.values, 
                                   feature_names=X.columns, 
                                   class_names=['rings'], 
                                   mode='regression',
                                   random_state=101)

然后，我们使用此解释器为我们的第一个预测创建一个解释器对象 exp（第 2-4 行）。最后，我们显示这个解释器对象（第 7 行）。此操作的输出就是你在 图 3 中看到的内容。通过设置 table=True，我们将表格包含在右侧。我们尚未为核宽度或代理模型等选项设置参数，因此包将使用默认值。

# 获取第一行的解释
exp = explainer.explain_instance(X.iloc[0], 
                                 model.predict, 
                                labels=X.columns)

#显示解释
exp.show_in_notebook(show_table=True)

图 3 为我们提供了有关第一个预测的大量信息。我们可以看到预测值为 12.98 个环。中间的图表告诉我们每个特征对预测的贡献。请注意，有 8 个条形图 — 每个特征一个。例如，对于这只鲍鱼，壳重量的值减少了预测环的数量。值 -1.20 是此特征的 LIME 权重。右侧的表格给出了特征值。

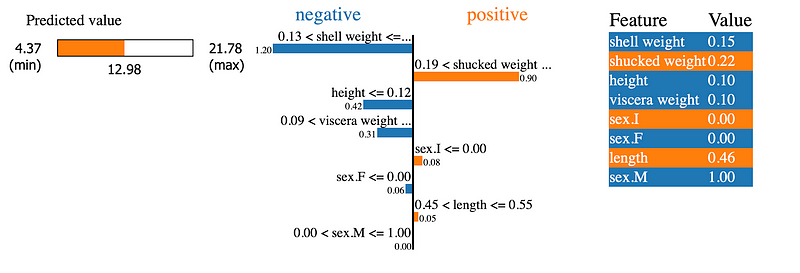
每个特征的 LIME 权重是替代模型的系数。与 SHAP 不同，权重和平均预测的总和不会等于给定实例的预测。你可以使用下面的代码来确认这一点。这是因为 LIME 并不“高效”。

# 检查计算
exp_weight = [x[1] for x in exp.as_map()[1]]

print(np.mean(y_pred) + sum(exp_weight)) 
print(y_pred[0]) 

---
9.64
12.68

此属性是 SHAP 的另一个优点。也就是说，如果你将每个模型特征的 SHAP 值与平均预测相加，则可以得到该实例的预测。换句话说，它们准确地告诉我们特征对预测的改变程度。这改善了对 SHAP 值的解释。使用 LIME，我们只知道方向和重要性。

充分利用 LIME（全局解释）

当你想了解单个预测是如何做出时，局部解释非常有用。但是，查看单个预测并不能告诉我们模型的总体工作原理。为此，我们可以使用不同的局部解释聚合。也就是说，我们将使用不同的图表组合多个预测的 LIME 权重。

首先，我们需要从解释器对象中获取 LIME 权重。为此，我们可以使用下面的函数return_weights。此函数接受一个解释器对象 exp。从此对象中，它将获取并返回一个 LIME 权重列表 exp_weight。这些权重将按照与 X 特征矩阵中的特征相同的顺序排序。

def  return_weights（exp）：
    
    """ 从 LIME 解释对象获取权重 """
    
    exp_list = exp.as_map()[1]
    exp_list = sorted(exp_list, key=lambda x: x[0])
    exp_weight = [x[1] for x in exp_list]
    
    return exp_weight

要使用此函数，我们将迭代 X 特征矩阵的前 100 行（第 4 行）。对于每次迭代，我们将创建一个解释对象（第 7-10 行）。我们使用 return_weights 函数从此对象获取权重（第 13 行），并将它们附加到权重列表中（第 14 行）。最后，我们使用此权重列表创建 DataFrame， 即 lime_weights（第 17 行）。

权重 = []

# 遍历特征矩阵中的前 100 行
for x in X.values[ 0 : 100 ]:
    
    # 获取解释
    exp = explainer.explain_instance(x, 
                                 model.predict, 
                                 num_features=10, 
                                labels=X.columns)
    
    # 获取权重
    exp_weight = return_weights(exp)
    weights.append(exp_weight)
    
# 创建数据框
lime_weights = pd.DataFrame(data=weights,columns=X.columns)

lime_weights 数据集的形状为 (100,8)。每行代表一个不同的预测。对于每个预测，8 个特征中的每一个都有一个 LIME 权重。我们现在可以使用此数据集创建 LIME 权重的全局聚合。

绝对平均值

第一个聚合可以帮助我们了解哪些特征最重要。具有高正或负 LIME 权重的特征对预测的影响更大。对于每个特征，我们可以取所有 LIME 权重的绝对平均值。一般来说，具有较大平均权重的特征对预测的贡献较大。

我们可以在图 4 中看到我们模型的平均权重。请注意，壳重和去壳重与其他特征相比具有更大的平均权重。这告诉我们，这些特征在预测环数时是最重要的。

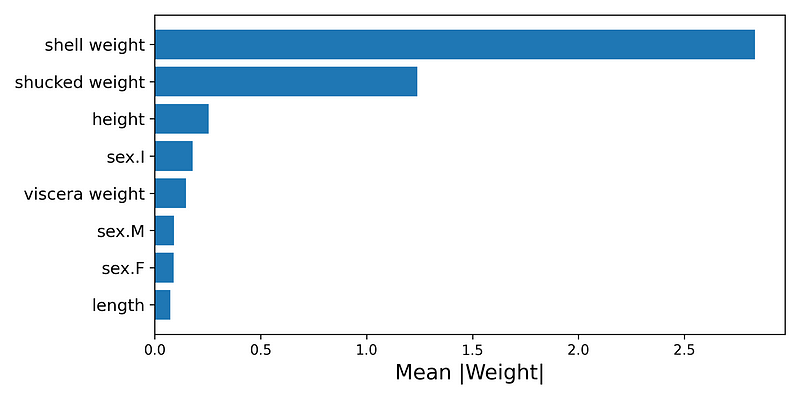
要创建此图表，我们首先取权重的绝对平均值（第 2 行）。然后，我们创建一个包含两列的新 DataFrame — 特征名称和绝对平均值（第 3 行）。我们将此 DataFrame 从最大到最小的平均权重排序（第 4 行）。最后，我们使用此 DataFrame 绘制条形图（第 9-11 行）。

# 获取 LIME 权重的绝对平均值
abs_mean = lime_weights.abs().mean(axis=0)
abs_mean = pd.DataFrame(data={'feature':abs_mean.index, 'abs_mean':abs_mean})
abs_mean = abs_mean.sort_values('abs_mean')

# 绘制绝对均值
fig, ax = plt.subplots(nrows=1, ncols=1,figsize=(8,4))

y_ticks = range(len(abs_mean))
y_labels = abs_mean.feature

plt.barh(y=y_ticks,width=abs_mean.abs_mean,)
plt.yticks(ticks=y_ticks,labels=y_labels,size= 12)
plt.title('')
plt.ylabel('')
plt.xlabel('Mean |Weight|',size=15)

特征趋势

我们还可以查看模型特征之一的趋势——整体重量。这是整只鲍鱼的重量。在图 5 中，我们可以看到，随着整体重量的增加，LIME 权重也会增加。更高的 LIME 权重表示，对于特定预测，特征值增加了预测的环数。因此，该图表告诉我们，随着鲍鱼重量的增加，其壳中的环数趋于增加。这是有道理的，因为我们认为年龄较大的鲍鱼会更大/更重。

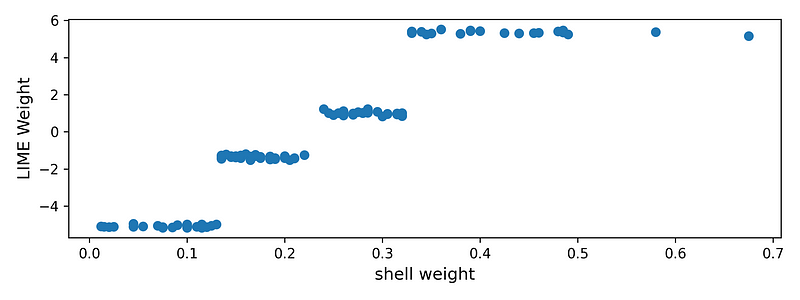
要创建此图表，我们首先获取整个重量特征的 LIME 权重（第 4 行）。我们还获取相应的特征值（第 5 行）。然后我们创建权重和特征值的散点图（第 7 行）。

fig, ax = plt.subplots(nrows=1, ncols=1,figsize=(8,3))

# 获取权重和特征值
feature_weigth = lime_weights['shell weight']
feature_value = X['shell weight'][0:100]

plt.scatter(x=feature_value ,y=feature_weigth)

plt.ylabel('LIME Weight',size=12)
plt.xlabel('shell weight',size=12)

蜂群

我们的最终聚合是一个蜂群图。如图6所示，这是所有 LIME 权重的图。值按 y 轴上的特征分组。对于每个组，点的颜色由相同特征的值决定（即，较高的特征值为红色）。特征按平均 LIME 权重排序。

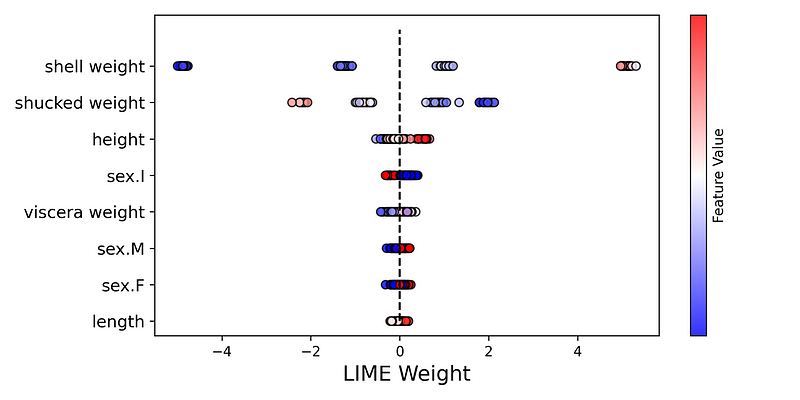
为了创建此图表，我们使用以下代码。为了给出概述，我们迭代每个特征（第 8 行）。对于每个特征，我们获得权重和值（第 10-11 行）。然后，我们使用这些创建散点图（第 13-18 行）。诀窍是将每个点的 y 值设置为相同的值（第 14 行）。这就是我们如何将散点图的每个点放在一条直线上。

fig, ax = plt.subplots(nrows=1, ncols=1,figsize=(8,4))

y_ticks = range(len(abs_mean))
y_labels = abs_mean.feature

# 为每个特征绘制散点图
for i,feature in enumerate(y_labels):
    
    feature_weigth = lime_weights[feature]
    feature_value = X[feature][0:100]
    
    plt.scatter(x=feature_weigth ,
                y=[i]*len(feature_weigth),
                c=feature_value,
                cmap='bwr',
                edgecolors='black',
               alpha=0.8)
    
plt.vlines(x=0,ymin=0,ymax=len(y_labels),colors='black',linestyles="--")
plt.colorbar(label='Feature Value',ticks=[])

plt.yticks(ticks=y_ticks,labels=y_labels,size=12)
plt.xlabel('LIME Weight',size=15)

如果你熟悉 SHAP 软件包，你会认出这些图。这些图的易用性和深刻见解是 SHAP 如此受欢迎的另一个原因。在整篇文章中，我们还解释了 SHAP 背后的理论如何产生理想的特性。最终，该软件包比 LIME 更易于使用，并提供更可靠的局部解释。

LIME 仍然很有用。在许多低风险应用中，解释的一致性并不那么重要。此外，正如我们所见，该理论相当简单。根据复杂模型的单个预测构建线性模型的想法可能并不难解释。这肯定比解释 SHAP 背后的理论更容易。

我们还提到 SHAP 的灵感来自 LIME。这是因为 SHAP 使用基于单个预测构建的线性模型来估计 Shapley 值。从这个意义上讲，SHAP 可以看作是 LIME 的一个特例，其中模型权重是 Shapley 值。这是使用特定内核实现的。最终，了解 LIME 可以帮助你了解 SHAP。

如果你有兴趣了解有关 SHAP 的更多信息，我后续将会写一些关于 SHAP 的文章。

其他更多的基础机器学习、神经网络内容，可以看看之前的「人工智能核心知识」，也可以看看下面这些系列文章：

「AI秘籍」系列课程：

• 人工智能应用数学基础
• 人工智能Python基础
• 人工智能基础核心知识
• 人工智能BI核心知识
• 人工智能CV核心知识

数据集

W. J Nash, et. al., 1994, Abalone Data Set, Irvine, CA: University of California, School of Information and Computer Science (License: CC0: Public Domain), https://archive.ics.uci.edu/ml/datasets/Abalone

参考

Ribeiro, M.T., Singh, S. and Guestrin, C., 2016 “Why should i trust you?” Explaining the predictions of any classifier. https://arxiv.org/abs/1602.04938

C. Molnar，Interpretable Machine Learning, 2021, https://christophm.github.io/interpretable-ml-book/lime.html

LIME Python 包，https://github.com/marcotcr/lime

SHAP Python 包，https://github.com/slundberg/shap